Southeast University：multiple wheeled mobile robots with application to cooperative transportation

Client: School of Automation, Southeast University

Paper Title:Embedded technique-based formation control of multiple wheeled mobile robots with application to cooperative transportation.

Application: Motion Capture, Robot Localization and Tracking, Robot Collaborative Control, Algorithm Validation, Wheeled Mobile Robots (WMRs), Control Engineering Practice (CEP).

Currently, the application of a single Wheeled Mobile Robot (WMR) in engineering transportation is quite common, but the collaborative transportation technology of multiple WMRs is still in the research and exploration phase. Many traditional collaborative control algorithms are designed directly based on the cooperative tracking error, and the design method based on this idea still has room for improvement in terms of complexity and flexibility.

With the advent of embedded control technology, improvements in these areas have become possible. Professor Wang Xiangyu's team at Southeast University proposed a collaborative transportation formation control algorithm using multiple WMRs, which was applied to solve the collaborative transportation problem of multiple WMRs. This paper has been published in the internationally renowned journal Control Engineering Practice.

1. Research Plan

The research team proposed a multi-WMR collaborative transportation formation control algorithm based on embedded technology. The algorithm consists of two parts: one part is the design of a distributed signal generator, which generates the desired trajectories for all WMRs; the other part is the design of a tracking controller, which enables the WMRs to follow their desired trajectories.

Advantages of the Algorithm:

1. Simplified Modular Design: Based on embedded technology, the proposed algorithm separates the dynamics of the WMRs and their communication topology. This allows the algorithm to be modularized into two relatively "decoupled" parts: the design of the distributed signal generator and the design of the tracking controller. This modular approach effectively reduces the complexity of the algorithm design.

   
   

2. Strong Compatibility: The algorithm can be applied to a variety of WMR collaborative transportation tasks, such as non-holonomic WMRs and omnidirectional WMRs. It also overcomes the encapsulation characteristics of WMRs, such as the inability to directly modify the working conditions of their controllers.

   
   

3. Finite Time Fast Formation: The algorithm includes a distributed signal generator and a tracking controller. The distributed signal generator converges within a finite time, and under the action of the tracking controller, the WMRs can follow their reference trajectories within a finite time. Thus, all WMRs can form the expected formation within a limited time.

   
   

2. Experimental Verification

The experiments were conducted in a 3.8m × 4.5m area. The research team carried out both formation experiments and collaborative transportation experiments. The experimental setup consisted of the CHINGMU motion capture system, three WMRs, and a transportation platform. Each WMR was equipped with an elevating device, STM32 F407, NVIDIA Jetson Xavier NX, and multiple markers. The WMRs formed an equilateral triangle with a side length of 0.8m and followed the leader. The transportation platform was set to a desired formation based on the WMRs' desired configuration, forming an equilateral triangle with a side length of 1m. The center of the equilateral triangle formed by the WMRs coincided with the center of the transportation platform, and their edges were parallel. The starting point of the desired trajectory of the transportation object coincided with the centroid of the WMRs' formation when the transportation started.

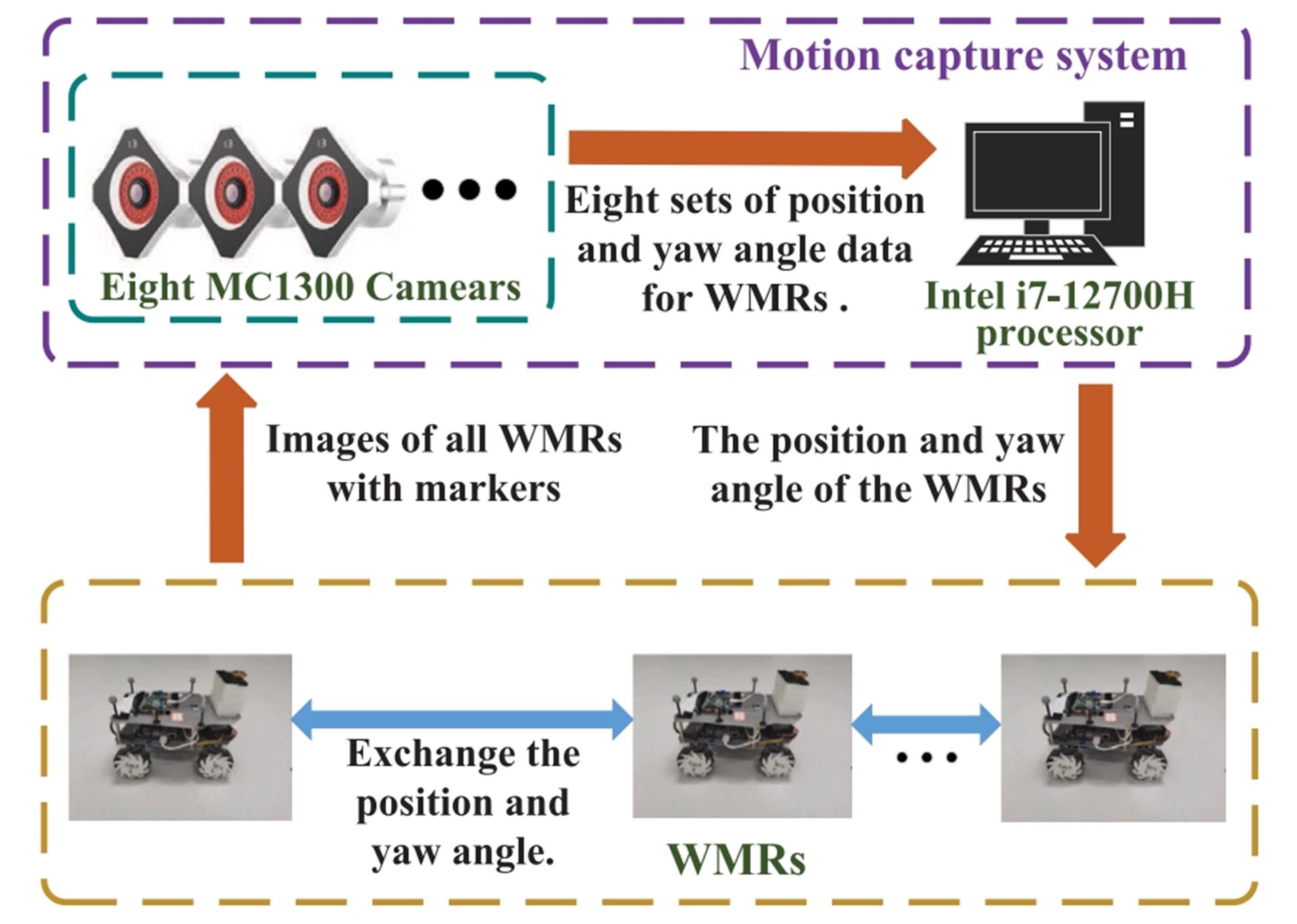
Figure 1: Data Flow Diagram of the Experimental Setup

Based on the sub-millimeter-level positioning and high-precision tracking advantages of the motion capture system, real-time data of the WMRs' positions, yaw angles, and travel trajectories were collected, providing precise data for algorithm validation and ensuring the experiment's authenticity.

Figure 2: Illustration of WMRs and the Transportation Platform

Figure 3: Communication Topology between the Leader and the WMRs

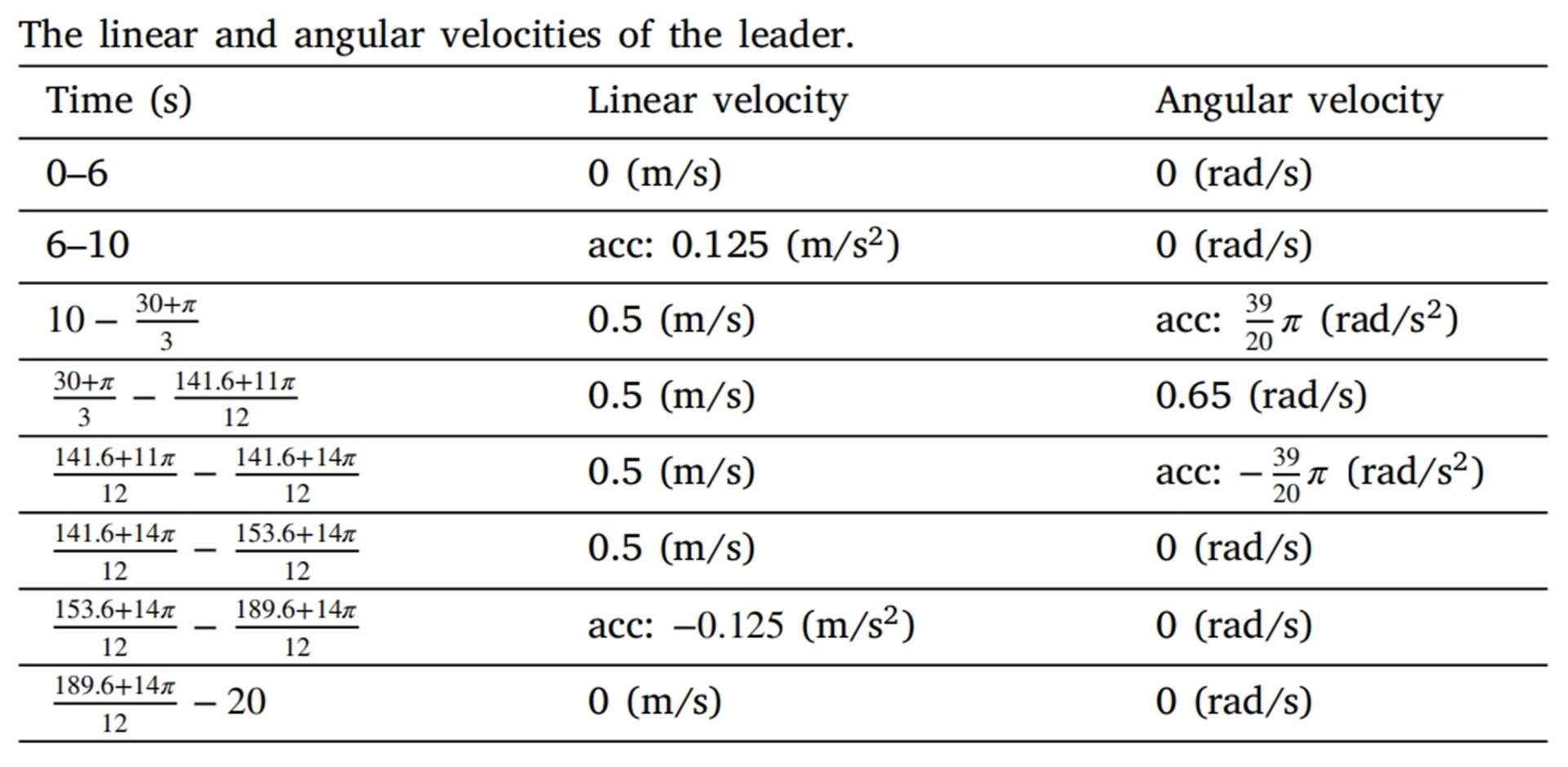
Table 1: Linear Velocity and Angular Velocity of the Leader

2.1 Formation Experiment

The three WMRs formed an equilateral triangle. Figure 4 shows that the initial positions of the WMRs were almost in a straight line, and within 5 seconds, they formed an equilateral triangle shape, which was maintained from 5 to 20 seconds. The response curve of the WMRs' distance tracking error is shown in Figure 5. Figure 6 presents the control inputs and the curves for (i=1, 2, 3), where it is evident that the control inputs were within reasonable limits.

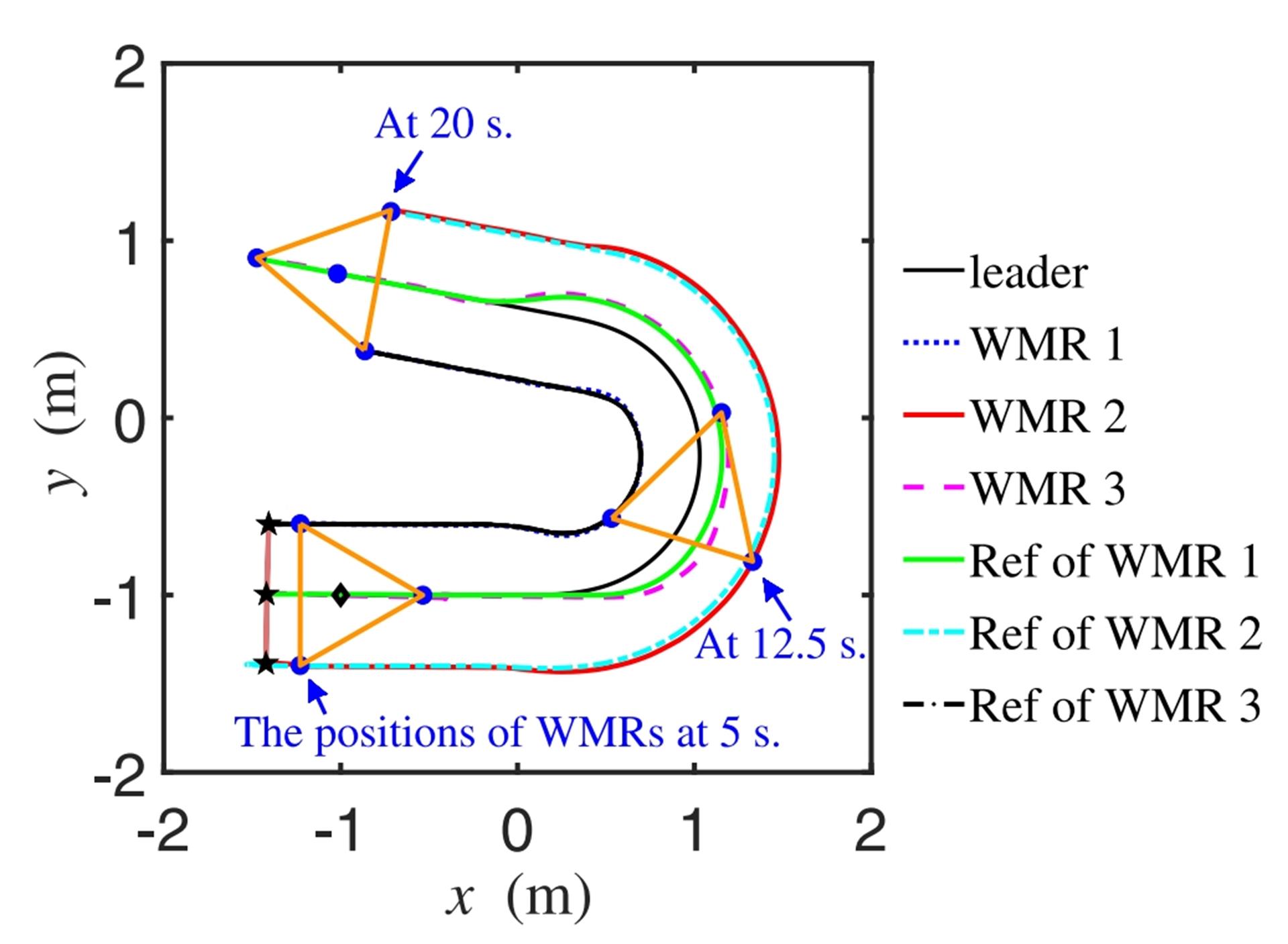
Figure 4: Reference and Actual Trajectories of the Leader and WMRs

Figure 5: Response Curve of the Distance Tracking Error

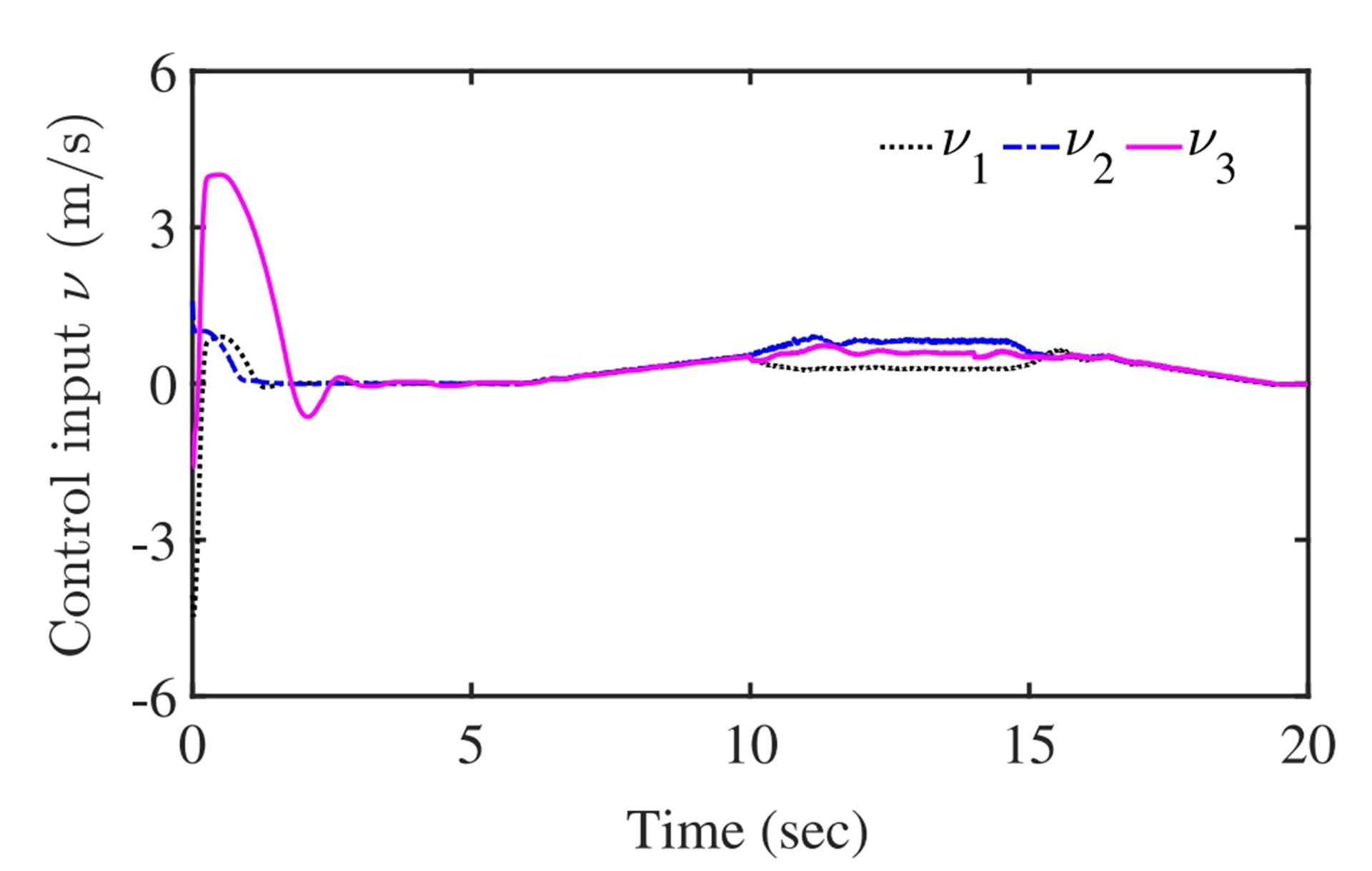
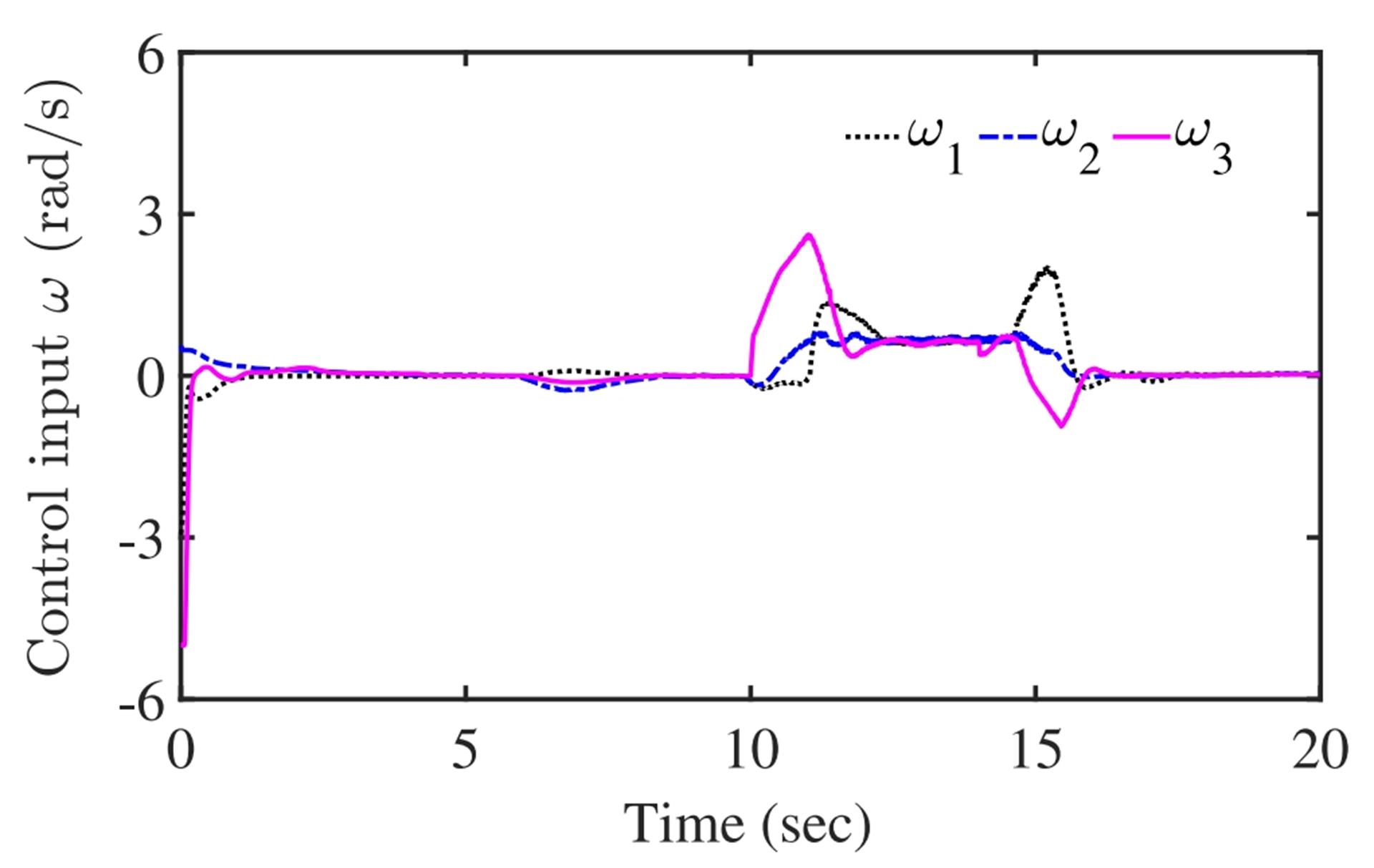
Figure 6: Time History of Control Inputs

2.2 Collaborative Transportation Experiment

The other settings in this experiment were the same as in the formation experiment. At the transportation starting point, when the WMRs formed the required formation, the transportation platform was installed, and the object was placed at the center of the platform. Subsequently, the WMRs maintained their desired formation while tracking the leader, transporting the object to the destination. Finally, the WMRs stopped at the destination with the expected formation.

Figures 7-9 show the experimental results. Figure 7 displays the reference trajectory of the WMRs and the actual trajectories of the leader and WMRs from 0 to 20 seconds. The position markers for the WMRs and the leader are consistent with Figure 4. Figures 8 and 9 show the response curve of the distance tracking error and the control inputs for (i=1, 2, 3), respectively.

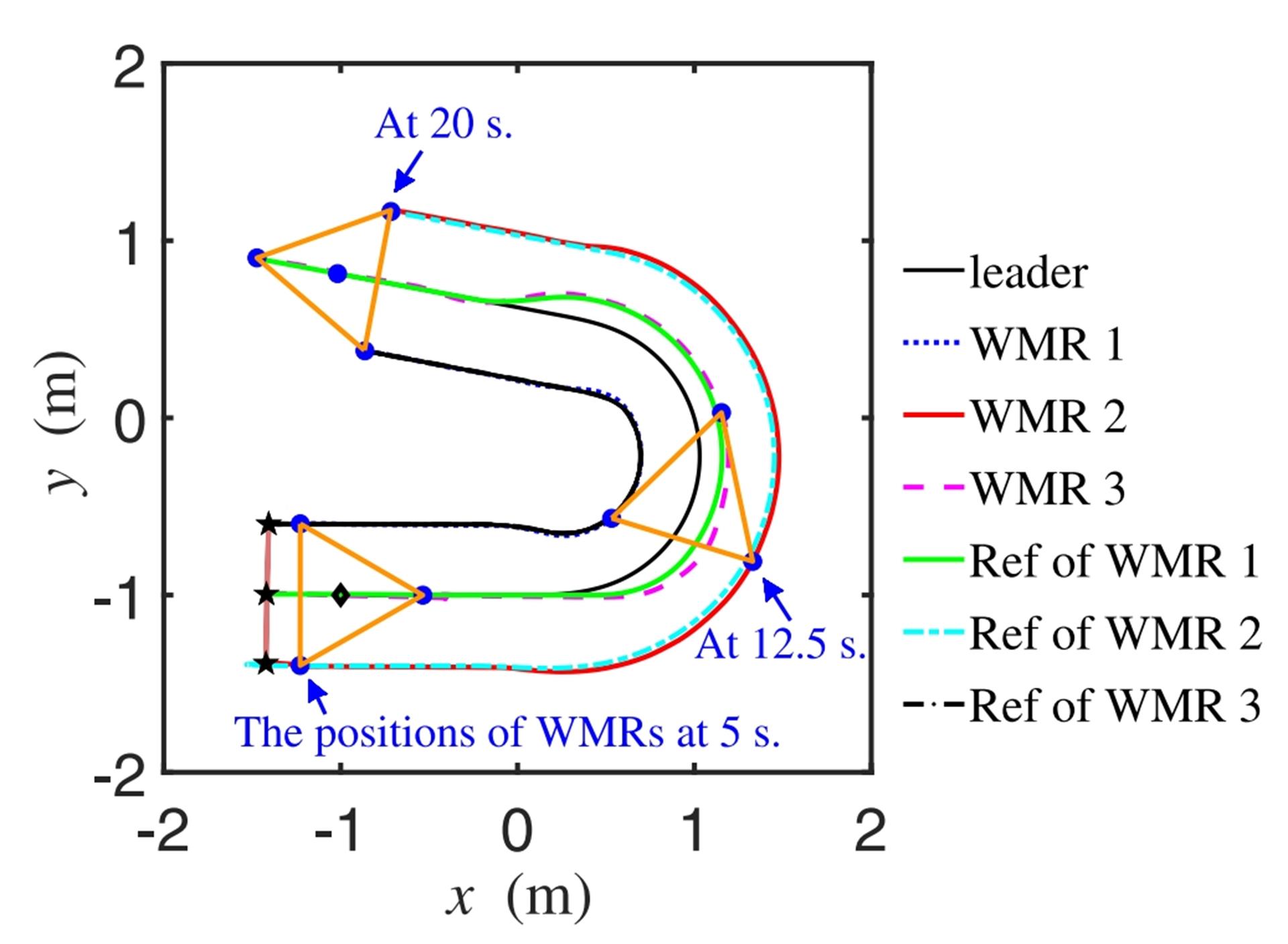
Figure 7: Reference and Actual Trajectories of the WMRs and Leader

Figure 8: Response Curve of the Distance Tracking Error

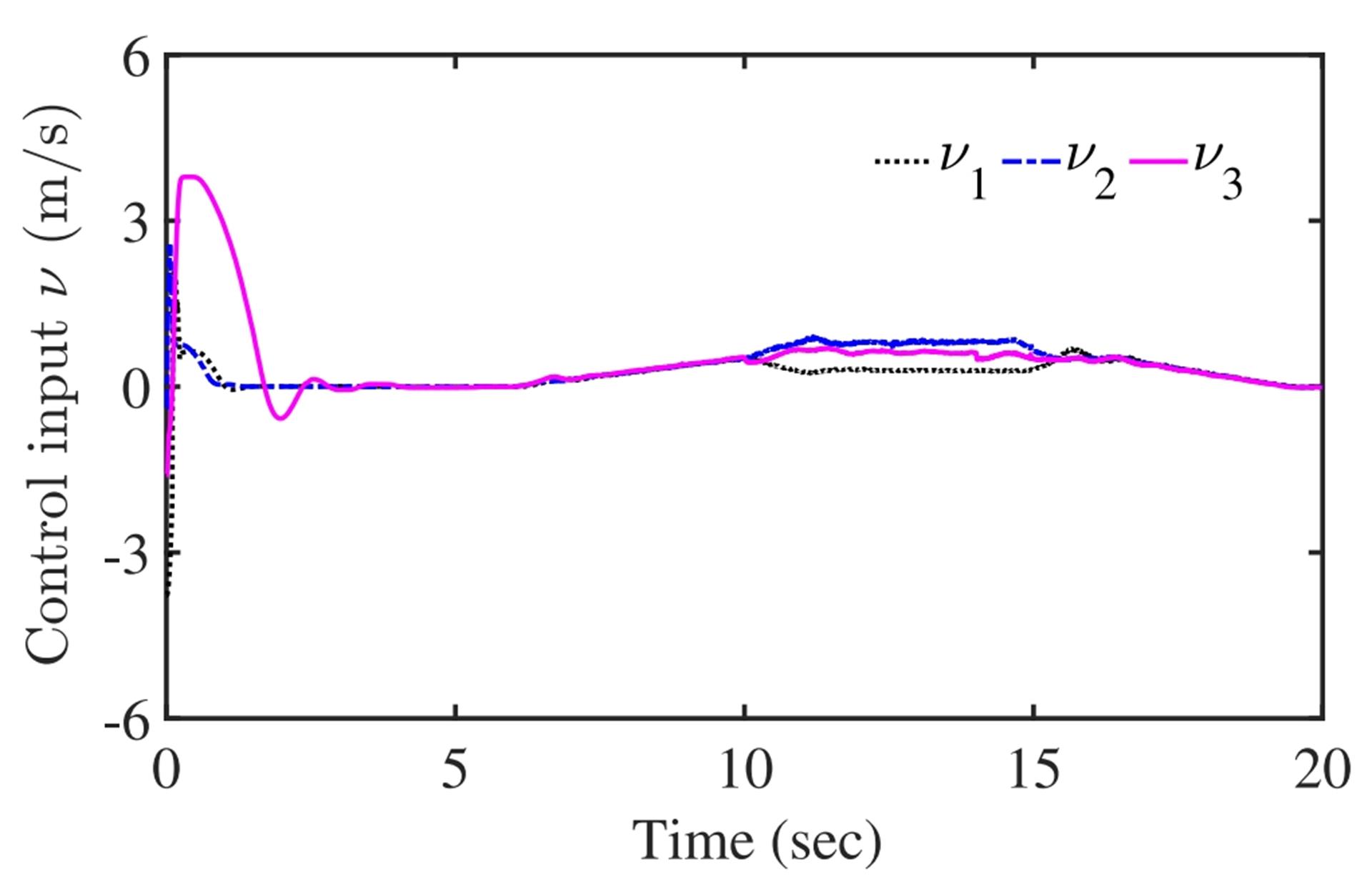
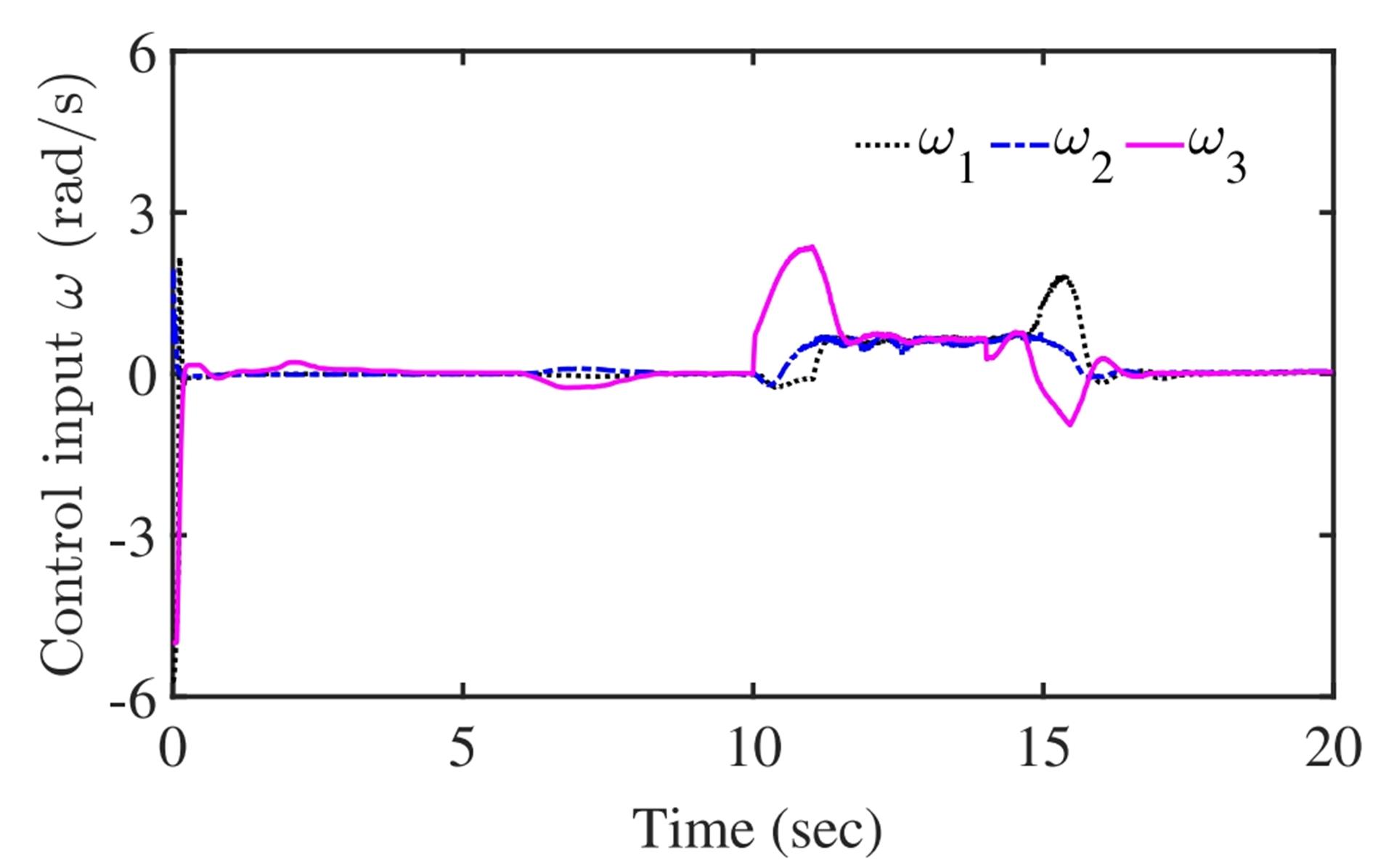
Figure 9: Time History of Control Inputs

3. Discussion of Experimental Results

The comparison of the two experiments is shown in Table 2. In the collaborative transportation experiment, the boundaries of the distance tracking errors for the WMRs were smaller than those in the formation experiment. The main reasons for this difference are twofold. First, the gravitational force of the object and the transportation platform indirectly increased the friction between the ground and the platform, providing a larger centripetal force during turns. Second, when the WMRs deviated too far from the desired position, they would make contact with the circular ring on the transportation platform, which provided a contact force to prevent further deviation. Despite the WMRs needing to provide centripetal force for the transportation platform and object during turns, the gravitational force of the object and platform enhanced the friction between the WMRs and the ground, which surpassed the need for centripetal force.

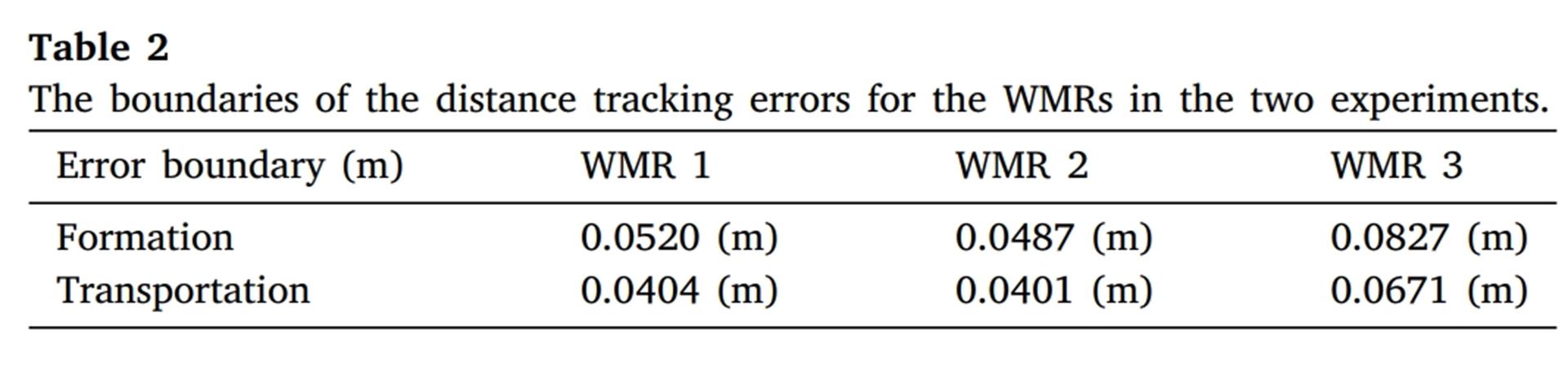
Table 2: Boundaries of Distance Tracking Errors in Both Experiments

4. Conclusion

This paper studied the multi-WMR collaborative transportation problem based on formation control. In the experimental platform, an embedded technology-based formation control algorithm was used to complete the collaborative transportation task. The algorithm can be developed in a general form, allowing the number of WMRs and formation configurations to be adjusted according to the weight and size of the transported object. The algorithm features a simplified modular design and strong compatibility, making it applicable to various industries and scenarios, such as logistics, smart factories, and more.

References

Ahmadabadi, M. N., & Nakano, E. (2001). A constrain and move approach to distributed object manipulation. lEEE Transactions on Robotics and Automation, 17(2), 157-172.

Alonso-Mora, J., Baker, S., & Rus, D. (2017). Multi-robot formation control and object transport in dynamic environments via constrained optimization. International Journal of Robotics Research,36(9),1000-1021.

Chen, Y., Chen, K., & Astolfi, A. (2022). Adaptive formation tracking control for first.order agents with a time-varying flow parameter. IEEE Transactions on Automatic Control, 67(5)，2481-2488.

Desai, J. P., Ostrowski, J. P., & Kumar, V. (2001). Modeling and control of formations of nonholonomic mobile robots. lEEE Transactions on Robotics and Automation, 17(6)905-908.

Ebel, H., Luo, W., Yu, F., Tang, Q., & Eberhard, P. (2021). Design and experimental validation of a distributed cooperative transportation scheme. IEEE Transactions on Automation Science and

Engineering, 18(3), 1157-1169.

Koung, D., Kermorgant, O., Fantoni, I., & Belouaer, L. (2021). Cooperative multi-robot object transportation system based on hierarchical quadratic programming. IEEE Robotics and Automation Letters, 6(4), 6466-6472.

Machado, T., Malheiro, T., Monteiro, S., Erlhagen, W., & Bicho, E. (2016). Multi-constrained joint transportation tasks by teams of autonomous mobile robots using a dynamical systems approach. In 2016 IEEE International Conference on Robotics and Automation (pp. 3111-3117). Stockholm, Sweden.

Ren, W., & Atkins, E. (2007). Distributed multi-vehicle coordinated control via local information exchange. International Journal of Robust and Nonlinear Control, 17, 1002-1033.

Wang, X., Wang, G., & Li, S. (2020). Distributed finite-time optimization for integrator chain multiagent systems with disturbances. IEEE Transactions on Automatic Control, 65(12), 5296- 5311.

Original link：

https://www.sciencedirect.com/science/article/abs/pii/S096706612400162X?via%3Dihub